Quickstart
[1]:
import immunowave as iw
import diffrax as dx
import numpy as np
import jax
import jax.numpy as jnp
import matplotlib as mpl
import matplotlib.pyplot as plt
jax.config.update("jax_enable_x64", True)
Define a model
FitzHugh-Nagumo + Bacteria
The dynamical variables \((A, B, R)\) denote the concentration of antimicrobial peptide, bacteria, and repression, respectively.
First we define a state by subclassing the abstract class immunowave.State.
[2]:
class FHNB_state(iw.State):
A: iw.ScalarField
B: iw.ScalarField
R: iw.ScalarField
Our dynamical field variables satisfy
Parameters:
\(\alpha\): Diffusion coefficient of antimicrobial peptide.
\(\theta\): Threshold for antimicrobial peptide production.
\(\eta\): Rate of antimicrobial peptide growth response to bacteria.
\(\rho\): Rate of antimicrobial peptide degradation response to repression.
\(\epsilon\): Rate of repression production.
\(\xi\): Diffusion coefficient of bacteria.
\(\lambda\): Rate of bacteria growth.
\(\mu\): Rate of bacteria death response to antimicrobial peptide.
Models are defined by subclassing the abstract class immunowave.Model, and implementing the right-hand side of the dynamical system by overriding the method immunowave.Model.__call__.
[3]:
class FHNB_model(iw.Model):
α: float
θ: float
η: float
ρ: float
ε: float
ξ: float
λ: float
μ: float
def __call__(self, t, state, args=None):
# unpack field variables
A, B, R = state.A, state.B, state.R
# unpack parameters
α, θ, η, ρ, ε, ξ, λ, μ = (
self.α,
self.θ,
self.η,
self.ρ,
self.ε,
self.ξ,
self.λ,
self.μ,
)
# define PDE
dAdt = α * A.laplacian(bc="neumann") + A * (A - θ) * (1 - A) + η * B - ρ * R
dBdt = ξ * B.laplacian(bc="neumann") + λ * B * (1 - B) - μ * A * B
dRdt = ε * (A - R)
return FHNB_state(dAdt, dBdt, dRdt)
Instantiate the model
[4]:
model = FHNB_model(α=1.0, θ=0.1, η=10.0, ρ=0.5, ε=0.1, ξ=0.1, λ=0.9, μ=0.1)
model
[4]:
FHNB_model(α=1.0, θ=0.1, η=10.0, ρ=0.5, ε=0.1, ξ=0.1, λ=0.9, μ=0.1)
Initialize fields
Spatial discretization
[5]:
L = 20.0
n = 200
shape = (n,)
lb = [0]
h = L / (n - 1)
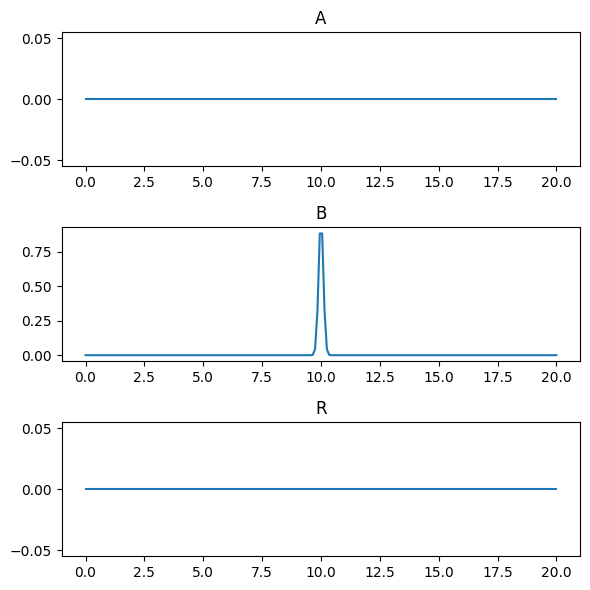
Initialize the \(A\) and \(R\) fields to zero and the \(B\) field to a finite impulse at the center of the domain.
[6]:
state = FHNB_state(
A=iw.ScalarField(shape, lb, h, 0),
B=iw.ScalarField(
shape, lb, h, fn=lambda x: 1 * jnp.exp(-((x - L / 2) ** 2) / (2 * 0.1**2))
),
R=iw.ScalarField(shape, lb, h, 0),
)
[7]:
axes = state.plot()
plt.show()
Solve
Define integration region
[8]:
t0 = 0.0
t1 = 30.0
Keyword arguments for the solver
[9]:
atol = 1e-6
rtol = 1e-6
kwargs = dict(
dt0=1e-4,
max_steps=10000000,
atol=atol,
rtol=rtol,
throw=True,
saveat=dx.SaveAt(dense=True),
)
Solve
[10]:
solution = iw.solve(model, state, t0, t1, **kwargs)
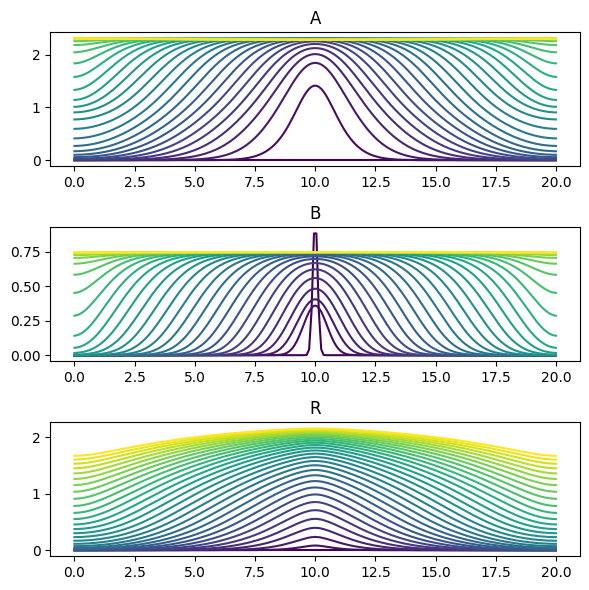
Plot
[11]:
for axis in axes:
axis.clear()
cmap = plt.cm.ScalarMappable(
norm=mpl.colors.Normalize(vmin=t0, vmax=t1), cmap=plt.cm.viridis
)
for t in np.linspace(t0, t1, int(t1 - t0) + 1):
axes = solution.evaluate(t).plot(axes=axes, color=cmap.to_rgba(t))
plt.show()
2D example
It is straightforward to extend the model to 2D or 3D. In fact, we can use the same model instance and state class as above, but change the state instance to a 2D or 3D domain. For 2D we update the domain parameters to:
[12]:
shape = (n, n)
lb = [0, 0]
h = L / (n - 1)
[13]:
state = FHNB_state(
A=iw.ScalarField(shape, lb, h, 0),
B=iw.ScalarField(
shape,
lb,
h,
fn=lambda x, y: jnp.exp(-((x - L / 2) ** 2 + (y - L / 2) ** 2) / (2 * 0.1**2)),
),
R=iw.ScalarField(shape, lb, h, 0),
)
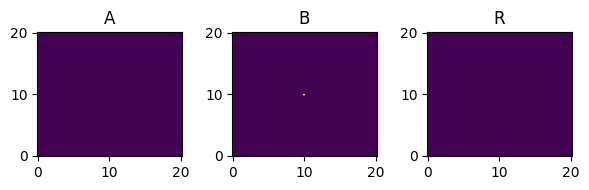
[14]:
fig, axes = plt.subplots(1, 3, figsize=(0.1 * 3 * L, 0.1 * L))
state.plot(axes=axes)
plt.show()
[15]:
time_grid = np.linspace(t0, t1, 11)
solution = iw.solve(
model, state, t0, t1, dt0=1e-2, max_steps=100000, saveat=dx.SaveAt(ts=time_grid)
)
[16]:
for i, time_point in enumerate(time_grid):
print(f"{time_point=}")
fig, axes = plt.subplots(1, 3, figsize=(6, 2))
solution.ys.plot(time_idx=i, vmin=0, vmax=1, axes=axes, cmap="turbo")
plt.show()
time_point=0.0
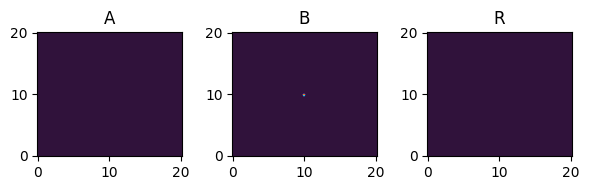
time_point=3.0
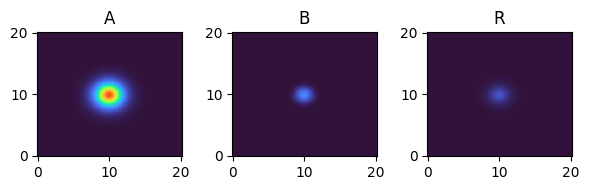
time_point=6.0
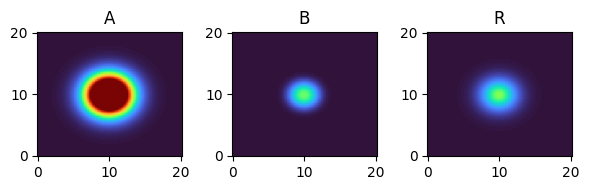
time_point=9.0
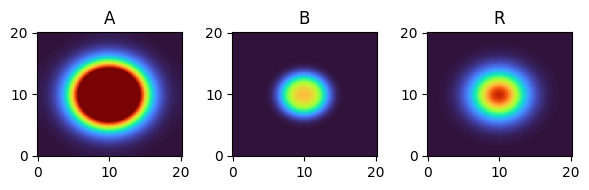
time_point=12.0
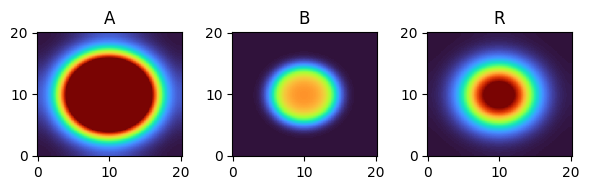
time_point=15.0
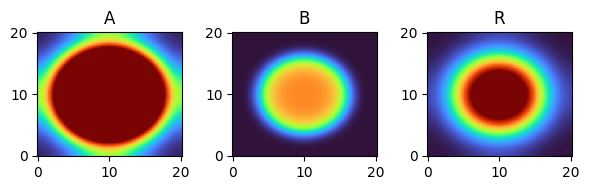
time_point=18.0
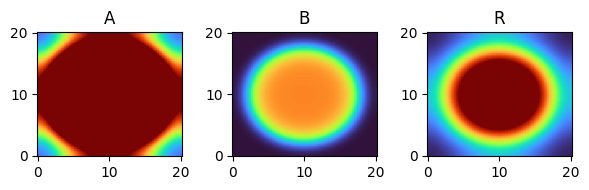
time_point=21.0
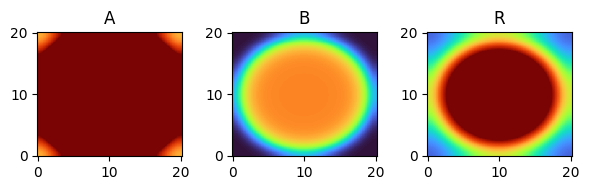
time_point=24.0
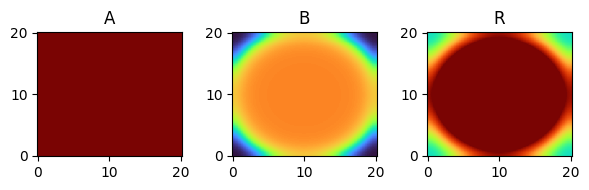
time_point=27.0
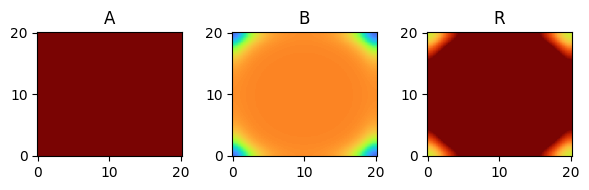
time_point=30.0
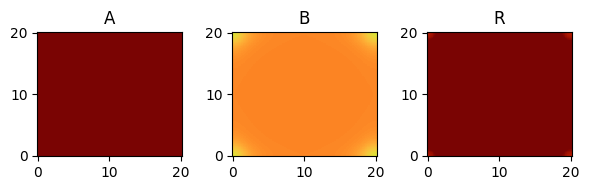
[ ]: