A dynamical perspective on triggering multiscale immune responses
Preprint: BH Schlomann, WS DeWitt, Y Zhang, K Shah. Ignition criteria for trigger waves in cell signaling.
arXiv:2508.16810 [q-bio.CB]
This work grew out of a “research jam” during Postdocs in Complexity meetings at the Santa Fe Institute (SFI), and was developed through two SFI-funded micro working groups with Brandon Schlomann, Yuanzhao Zhang, Kasturi Shah, and me (Will). Brandon led us on an adventure motivated by the question: how do cell signaling processes—such as innate immune mechanisms—balance local and global excitations? Local cellular activation of immune factors may be insufficient to control a proliferating immune challenge. On the other hand, while global tissue-scale activation more robustly suppresses threats, such inflammation is also damaging to healthy tissue.
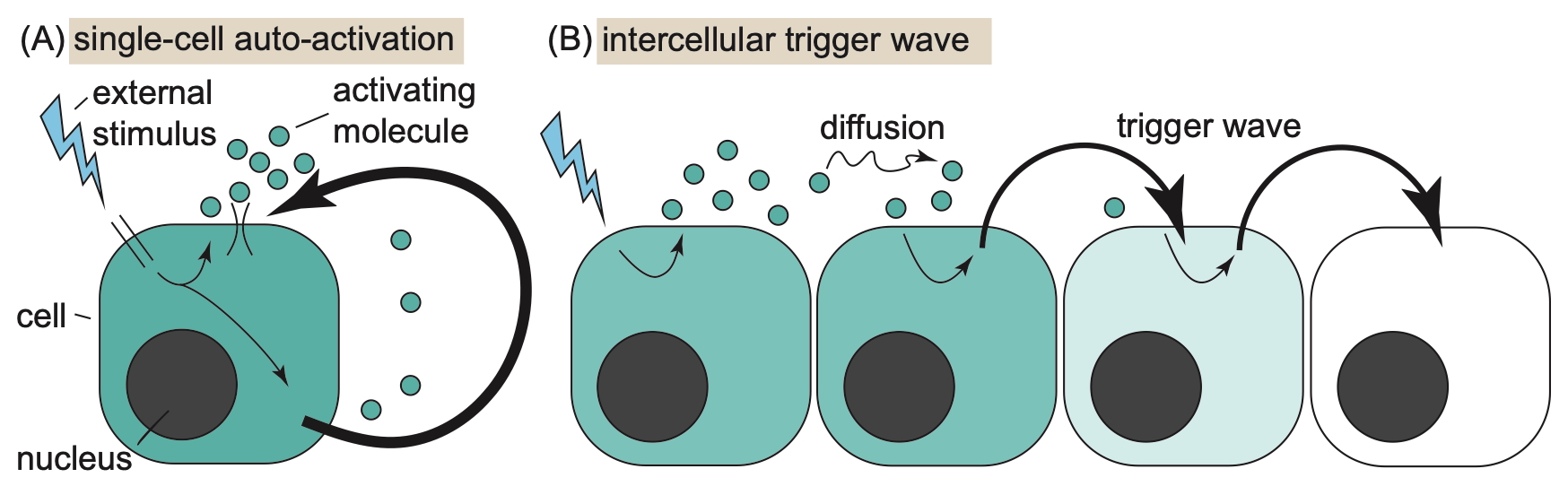
We study a dynamical model of local stimulus and spatially distributed response with biophysical (Hill function) autoactivation. Our dynamical variable $u(x,t)$, representing an extracellularly diffusing immune response factor, satisfies the non-dimensionalized equation
\[\partial_t u = \nabla^2 u + f(u) + 2 I \delta,\]where
\[f(u) = \frac{u^n}{K_D^n + u^n} - u,\]models autoactivation and decay, with $K_D > 0$, $n > 1$. $I$ denotes the intensity of the local stimulus (e.g. an infection), and $\delta(x)$ a Dirac mass localizing the stimulus to the origin.
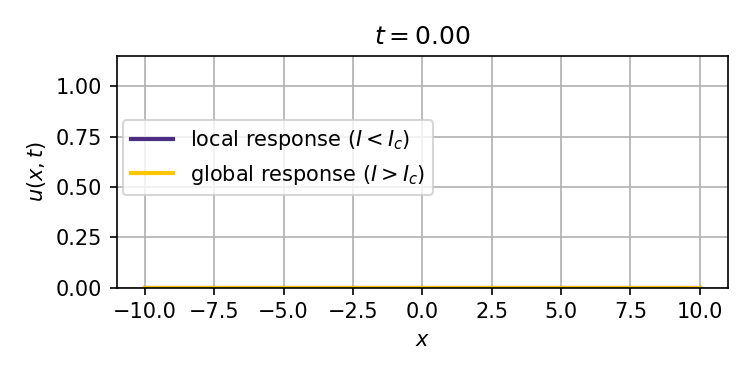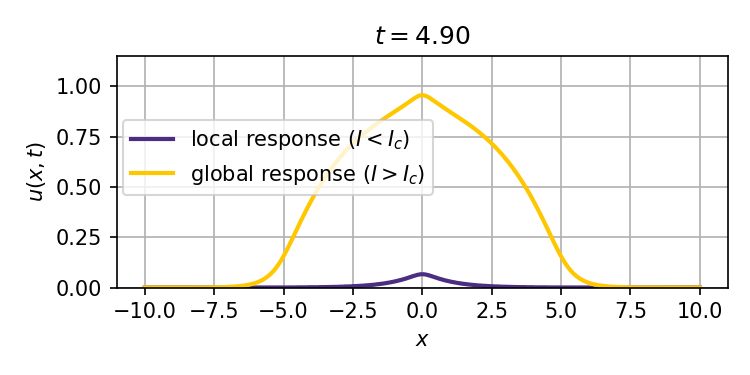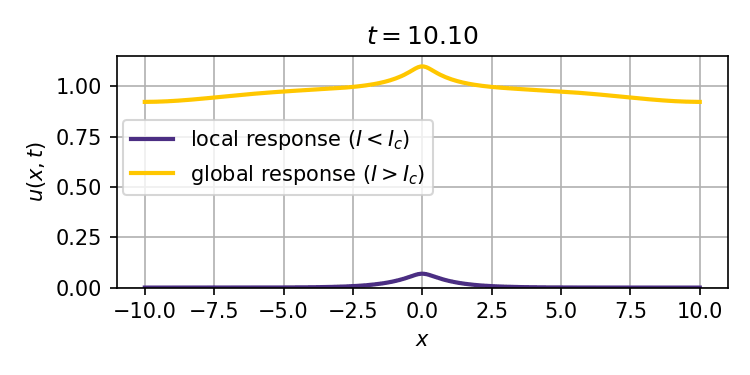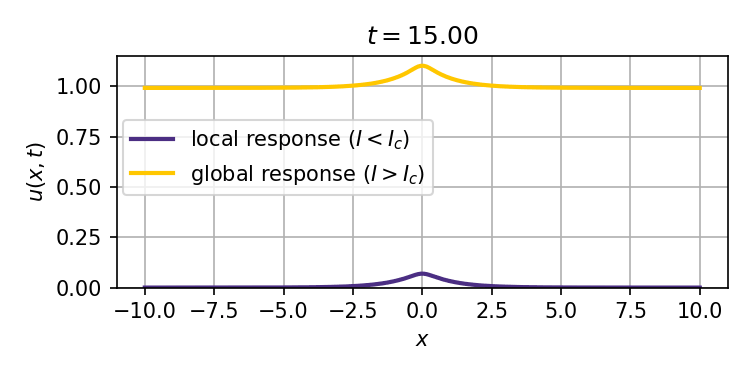
This system admits two stable stationary states: a weak stimulus $I<I_c$ will result in a localized response that decays exponentially with distance from the site of the stimulus, while a strong enough stimulus $I>I_c$ can ignite a trigger wave that spreads the response to the entire spatial domain (tissue).
We obtain analytical and numerical results for how the critical stimulus $I_c$ scales with the autoactivation circuit parameters $K_D$ (effective dissociation constant) and $n$ (Hill coefficient). This scaling as $K_D^\frac{n}{n-1}$ is the same in 1, 2, and 3 spatial dimensions, and suggests the potential to predict ignition thresholds from experiments that provide bulk activation measurements, and thus inform synthetic biology designs for trigger wave systems.
Brandon Schlomann was the creative force behind this work, even digging into mathematical literature on “autowaves” only available in Russian (which none of us can read) for hints at analytical techniques for our ignition threshold.
Bonus: We developed a Python software package immunowave to facilitate the exploration of these dynamics. It is quite general and may be applied to study triggering phenomena in fairly arbitrary systems. We built this on Patrick Kidger’s excellent Diffrax package.

Comments